Cracker Barrel Data Science
02 May 2020As a kid growing up in South-West Louisiana, my family spent a few weeks every winter in West Texas camping and hunting deer. A regular occurrence of these trips was eating at Cracker Barrel. Having spent the whole morning sitting in the woods alone and missing my N64, I got obsessed with the “jump all but one” game present on every table.

The the game begins by placing a tee in every hole except one (of your choice). You then “jump” the tees (similar to checkers) until no jumps can be made. The goal is to leave just one tee. The more tees you leave on the board, the more “ignorant” you are (as the rules state). Given that we went there so often, I was able to work out a solution and memorized it. I liked challenging myself every following year to see if I could remember the solution (or resynthesize it).
I went back to Cracker Barrel recently for the first time in 15 years. The game was still there. I gave solving it a shot but left 2 tees on the board. While I was playing, a lot of questions were going through my head. Stuff like:
- Out of all possible games, how are they distributed? Is leaving one tee really that rare? It almost seemed harder to leave more than 4.
- Does it matter where you leave the first hole?
- How hard is it for the last tee to land in the hole you started with? (something I could do as a kid)
I realized that there probably aren’t that many possible games and we should be able to brute force some of these answers by simulating the game and enumerating every possible move. Perhaps there are purely analytical answers to these questions, but I’m personally able to express this much more easily in code than in math.
Creating a notation
For some reason, I got the itch to start this while I was in a cabin in Mississippi without my computer. So the first thing I did was write down a notation and a set of legal moves on a bookmark and I snapped a pic of it with my phone.
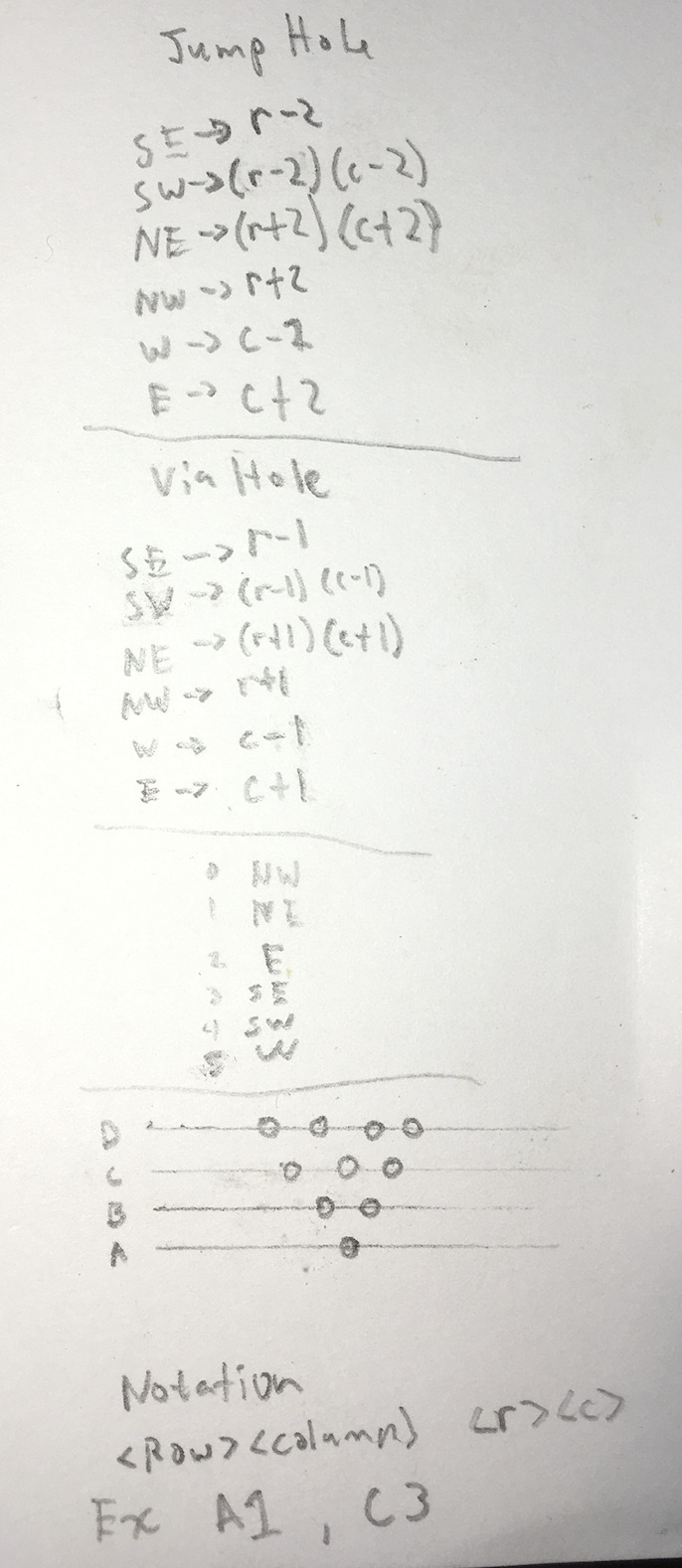
I chose a notation similar to chess (rank and file). The common board orientation will be with one of the tips of the triangle pointing at you. So each row will be labeled going up (A, B, C, D, E) and each column (1,2,3,4,5).
Because we will be storing the positions in a 2D list, we need a way to store positions and convert them to and from their cartesian point system and their chess-like notation.
@dataclass
class Position:
file: int
rank: int
@staticmethod
def from_str(pos):
f, r = list(pos)
r = int(r) - 1
f = ord(f) - 97
return Position(f, r)
def __repr__(self):
return "%s%s" % (chr(self.file + 97), self.rank + 1)Example use:
p = Position.from_str('b2')
print(p.file) #=> 1
print(p.rank) #=> 1
print(p) #=> b2The Game object will then be constructed with an open_position (the hole you are leaving open).
There will be a _board variable which contains the 2D list of Holes which are either filled or not.
class Hole:
def __init__(self, pos):
self.position = pos
self.filled = True
class Game:
def __init__(self, open_position='a1'):
self._board = []
rank = 5
file = 1
for r in range(rank):
self._board.append([Hole(Position(f, r)) for f in range(file)])
file += 1
self._hole_at(Position.from_str(open_position)).filled = False
self.moves = []
# Allows us to fetch a hole at a position
def _hole_at(self, pos):
if pos.rank >= 0 and pos.rank < len(self._board):
rank = self._board[pos.rank]
if pos.file >= 0 and pos.file < len(rank):
return rank[pos.file]
def __repr__(self):
s = []
for r in reversed(range(len(self._board))):
s.append("".join(["x" if hole.filled else "o" for hole in self._board[r]]))
return "\n".join(s)Example use. The game pretty-prints an ASCII board:
print(Game())
#=> xxxxx
#=> xxxx
#=> xxx
#=> xx
#=> oWe now need a way to encode the rules of the game, and a way to get from one game state to another. First let’s describe the directions which a piece may possibly move as an Enum:
class Direction(Enum):
NW = 0
NE = 1
E = 2
SE = 3
SW = 4
W = 5We can encode a “move” in the game as an object with 2 positions:
@dataclass
class Move:
start: Position
end: Position
def __repr__(self):
return "%s %s" % (self.start, self.end)Even though there are 6 directions a peg may move, certain holes limit which direction a peg can move. For instance, from the tip of the pyramid, only 2 directions are possible.
Instead of calculating this during the runtime of the game, I decided to encode all possible “jumps” into each hole.
class Hole:
def __init__(self, pos):
# ...
self.jumps = {}
@dataclass
class Jump:
via: Hole
dest: Hole
def is_valid(self):
return self.via.filled and not self.dest.filled
class Game:
def __init__(self, open_position='a1', rank=5):
# ...
self._build_jumps()
# ...
def _build_jump(self, direction, rank, file):
via = None
dst = None
if direction == Direction.NW:
via = self._hole_at(Position(file, rank+1))
dst = self._hole_at(Position(file, rank+2))
if direction == Direction.NE:
via = self._hole_at(Position(file+1, rank+1))
dst = self._hole_at(Position(file+2, rank+2))
if direction == Direction.E:
via = self._hole_at(Position(file+1, rank))
dst = self._hole_at(Position(file+2, rank))
if direction == Direction.SE:
via = self._hole_at(Position(file, rank-1))
dst = self._hole_at(Position(file, rank-2))
if direction == Direction.SW:
via = self._hole_at(Position(file-1, rank-1))
dst = self._hole_at(Position(file-2, rank-2))
if direction == Direction.W:
via = self._hole_at(Position(file-1, rank))
dst = self._hole_at(Position(file-2, rank))
if via and dst:
return Jump(via, dst)
def _build_jumps(self):
for rank in range(len(self._board)):
for file in range(len(self._board[rank])):
for direction in Direction:
jmp = self._build_jump(direction, rank, file)
if jmp:
self._board[rank][file].jumps[direction] = jmpNow we need a way to calculate which moves are valid and the ability to make them:
class Game:
#...
def move(self, move):
src_hole = self._hole_at(move.start)
dst_hole = self._hole_at(move.end)
jump = [jmp for jmp in src_hole.jumps.values() if jmp.dest == dst_hole][0]
if jump.is_valid():
src_hole.filled = False
jump.via.filled = False
dst_hole.filled = True
self.moves.append(move)
else:
raise Exception('Invalid move')
def valid_moves(self):
moves = []
for rank in self._board:
for hole in rank:
if hole.filled:
for jmp in hole.jumps.values():
if jmp.is_valid():
moves.append((hole, jmp))This should be enough to play the game:
g = Game()
print(g)
#=> xxxxx
#=> xxxx
#=> xxx
#=> xx
#=> o
p1 = Position.from_str('c3')
p2 = Position.from_str('a1')
g.move(Move(p1, p2))
print(g)
#=> xxxxx
#=> xxxx
#=> xxo
#=> xo
#=> xNow that we can play a game, we need some code to play every possible game. We’ll do this by doing a depth-first search through every move. At each “branchng” in this tree of moves, we’ll clone the game state and the moves we made so far so we can save all the games in memory.
I’ve decided to call this thing that plays all possible games a “Session” due to lack of creative energy:
class Game:
# ...
def clone(self):
return copy.deepcopy(self)
class Session:
def __init__(self):
self.log = []
def walk(self, game=Game()):
mvs = game.valid_moves()
if not mvs:
if (len(self.log) % 10000 == 0):
print("Completed Games: %d" % len(self.log))
self.log.append(game.clone())
return
for move in mvs:
start, jmp = move
checkpoint = game.clone()
# Make the move
game.move(Move(start.position, jmp.dest.position))
# Perform all other future moves in this branch
self.walk(game)
# restore the game from checkpoint and execute next move
game = checkpointYou run the session like so:
sess = Session()
sess.walk()And now sess.log contains all possible games.
print(len(sess.log))
#=> 568630So it appears there are 568630 possible games that start with this configuration.
What about the distribution of scores?
def remaining_tees(game):
holes = [hole for rank in game._board for hole in rank]
return len(list(filter(lambda h: h.filled, holes)))
tees = np.array(list(map(remaining_tees, sess.log)))
plt.hist(tees, bins=np.arange(tees.min(), tees.max()+1))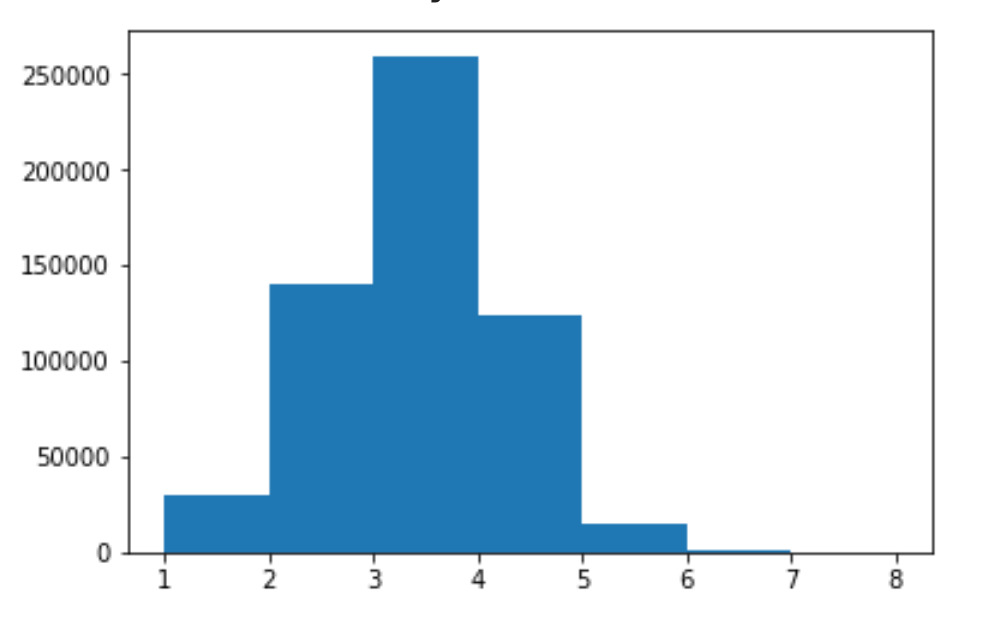
In number of tees remaining:
- 29760 (5.2% of games)
- 139614 (24.5% of games)
- 259578 (45.6% of games)
- 123664 (21.7% of games)
- 14844 (2.6% of games)
- 844 (0.1% of games)
- 326
What’s pretty interesting is that there are 2 games that end in 8:
games = list(filter(lambda g: remaining_tees(g) == 8, sess.log))
len(games)
#=> 2
games[0]
#=> xxxxx
#=> oooo
#=> xxx
#=> oo
#=> o
games[1]
#=> xxxxx
#=> oooo
#=> xxx
#=> oo
#=> oHere are the moves to achieve those game states:
games[0].moves
#=> [a3 a1, c5 a3, d4 b4, a4 c4, c3 c5, a1 c3]
games[1].moves
#=> [c3 a1, c5 c3, a4 c4, d4 b4, a3 c5, a1 a3]We now have a framework for analyzing the game. Below is the full code (it’s meant to be run in a Jupyter notebook):
%pylab inline
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import scipy
import numpy as np
from scipy.stats import beta
import pandas as pd
import math
from enum import Enum
from dataclasses import dataclass
import random
import copy
class Direction(Enum):
NW = 0
NE = 1
E = 2
SE = 3
SW = 4
W = 5
@dataclass
class Position:
file: int
rank: int
@staticmethod
def from_str(pos):
f, r = list(pos)
r = int(r) - 1
f = ord(f) - 97
return Position(f, r)
def __repr__(self):
return "%s%s" % (chr(self.file + 97), self.rank + 1)
@dataclass
class Move:
start: Position
end: Position
def __repr__(self):
return "%s %s" % (self.start, self.end)
class Hole:
def __init__(self, pos):
self.position = pos
self.filled = True
self.jumps = {}
@dataclass
class Jump:
via: Hole
dest: Hole
def is_valid(self):
return self.via.filled and not self.dest.filled
class Game:
def __init__(self, open_position='a1', rank=5):
self._board = []
file = 1
for r in range(rank):
self._board.append([Hole(Position(f, r)) for f in range(file)])
file += 1
self._hole_at(Position.from_str(open_position)).filled = False
self._build_jumps()
self.moves = []
def move(self, move):
src_hole = self._hole_at(move.start)
dst_hole = self._hole_at(move.end)
jump = [jmp for jmp in src_hole.jumps.values() if jmp.dest == dst_hole][0]
if jump.is_valid():
src_hole.filled = False
jump.via.filled = False
dst_hole.filled = True
self.moves.append(move)
else:
raise Exception('Invalid move')
def valid_moves(self):
moves = []
for rank in self._board:
for hole in rank:
if hole.filled:
for jmp in hole.jumps.values():
if jmp.is_valid():
moves.append((hole, jmp))
return moves
def clone(self):
return copy.deepcopy(self)
def _hole_at(self, pos):
if pos.rank >= 0 and pos.rank < len(self._board):
rank = self._board[pos.rank]
if pos.file >= 0 and pos.file < len(rank):
return rank[pos.file]
def _build_jump(self, direction, rank, file):
via = None
dst = None
if direction == Direction.NW:
via = self._hole_at(Position(file, rank+1))
dst = self._hole_at(Position(file, rank+2))
if direction == Direction.NE:
via = self._hole_at(Position(file+1, rank+1))
dst = self._hole_at(Position(file+2, rank+2))
if direction == Direction.E:
via = self._hole_at(Position(file+1, rank))
dst = self._hole_at(Position(file+2, rank))
if direction == Direction.SE:
via = self._hole_at(Position(file, rank-1))
dst = self._hole_at(Position(file, rank-2))
if direction == Direction.SW:
via = self._hole_at(Position(file-1, rank-1))
dst = self._hole_at(Position(file-2, rank-2))
if direction == Direction.W:
via = self._hole_at(Position(file-1, rank))
dst = self._hole_at(Position(file-2, rank))
if via and dst:
return Jump(via, dst)
def _build_jumps(self):
for rank in range(len(self._board)):
for file in range(len(self._board[rank])):
for direction in Direction:
jmp = self._build_jump(direction, rank, file)
if jmp:
self._board[rank][file].jumps[direction] = jmp
def _coords(self, pos):
f, r = list(pos)
r = int(r) - 1
f = ord(f) - 97
return f, r
def __repr__(self):
s = []
for r in reversed(range(len(self._board))):
s.append("".join(["x" if hole.filled else "o" for hole in self._board[r]]))
return "\n".join(s)
class Session:
def __init__(self):
self.log = []
def walk(self, game=Game()):
mvs = game.valid_moves()
if not mvs:
if (len(self.log) % 10000 == 0):
print("Completed Games: %d" % len(self.log))
self.log.append(game.clone())
return
for move in mvs:
start, jmp = move
checkpoint = game.clone()
# Make the move
game.move(Move(start.position, jmp.dest.position))
# Perform all other future moves in this branch
self.walk(game)
# restore the game from checkpoint and execute next move
game = checkpoint